Extra Credit #1
Begins Oct 12, 2020
Ends Oct 23, 2020
The purpose of this assignment is to allow students to demonstrate their understanding of various abstract and applied physics topics. Because of the nature of this assignment, it will be graded fairly strictly—pay close attention to the Notes below. Assignments which are not completed as required will not be evaluated.
NOTES:
- The Extra Credit Assignment consists of four problems, to be completed outside of class. You will have TWO #4s to choose from. Do one or the other but not both.
- This assignment is Extra Credit and not required.
- This assignment is intended to provide students with the opportunity to review some of the material we've covered, and not all students need the same amount of review. Students will be eligible to receive credit on problems completed according to the table below.
| Your Test Average (incl. Ch 5-6 test) | Review Problems You Are Eligible to Complete |
| 0 - 79% |
Problems #1 - 4 |
| 80 - 89% |
Problems #2 - 4 |
| 90 - 100% |
Problems #3 - 4 |
| | |
- The total points earned by a student on this assignment will be determined by the instructor based on a number of factors, including number of problems completed, difficulty of problem, and overall quality of assignments submitted by students.
- You may work on the problems with other people—in fact, this is encouraged—but each person must complete his or her own assignment to be turned in. Even when numeric answers to problems are the same, solutions from different students must be written independently, and differently, and developed and explained in each student's own words.
- The assignment must have a separate cover sheet that includes your Name, Date, Course and Period, Name of Assignment and the specific numbers attempted. Staple this cover sheet to the front of the packet.
- Each response must be hand-written on a separate piece of paper, which must include:
a) Your name and the problem number at the top of the page.
b) Salient details from the original question written out as appropriate.
c) Your solution, hand-written in blue or black ink (pencil is OK as long as it's DARK), with all work shown in detail.
d) Drawings, diagrams, or graphs with labels must be used to explain your solution more clearly.
e) Written explanations (blurbs, in English) explaining important steps in your solution.
f) The final answer, with a box around it.
See below for an example.
If this seems like an awful lot of work, it is! Remember that this is Extra Credit: you're trying to impress the instructor with how well you can do. If in doubt, do a little more than you think you should, rather than trying to get by with less, at the risk of losing points on your solution.
- The assignment will be available online on Wednesday, Oct 12.
- The instructor will be available to answer questions about the assignment on a limited basis: before school, after school, and possibly by e-mail. The instructor will not be able to help you if you leave all of your work until the night before the assignment is due.
- Your completed assignment must be turned in to Google Classroom anytime before 3:00 PM on Friday, October 23, 2020.
EXAMPLE PROBLEM AND SOLUTION:
SAMPLE PROBLEM:
In "The Matrix," Neo is given a test by Morpheus, who asks him to leap from the top of one building to another. Assume the buildings are each 100m tall, and 15m apart. Neo runs and leaps from the first building with a velocity of 5.00 m/s at an angle of 36.9 degrees (toward the second building).
a. Will he make it to the next building?
b. Where exactly will Neo land?
(Assume no air friction in this problem.)

EXTRA CREDIT PROBLEMS
1. Volleyball Serve
Watch the video of Becca Hanel serving a volleyball. Using time data taken from the video (which runs at 30 frames per second) and reasonable distance/length estimations, calculate the initial velocity of the ball as it is served.
Carefully explain and document your reasoning, in words and calculations.
2. Motorcycle's Coefficient of Friction
In the 2012 MotoGP race in Silverstone England, TV coverage provided data for some motorcycles' position on the racetrack and speed at that location (see video clip). By taking some screenshots, searching on Google Maps for the racetrack, and using Adobe Photoshop layers, I (Mr. White) was able to do some additional graphical analysis (shown here).
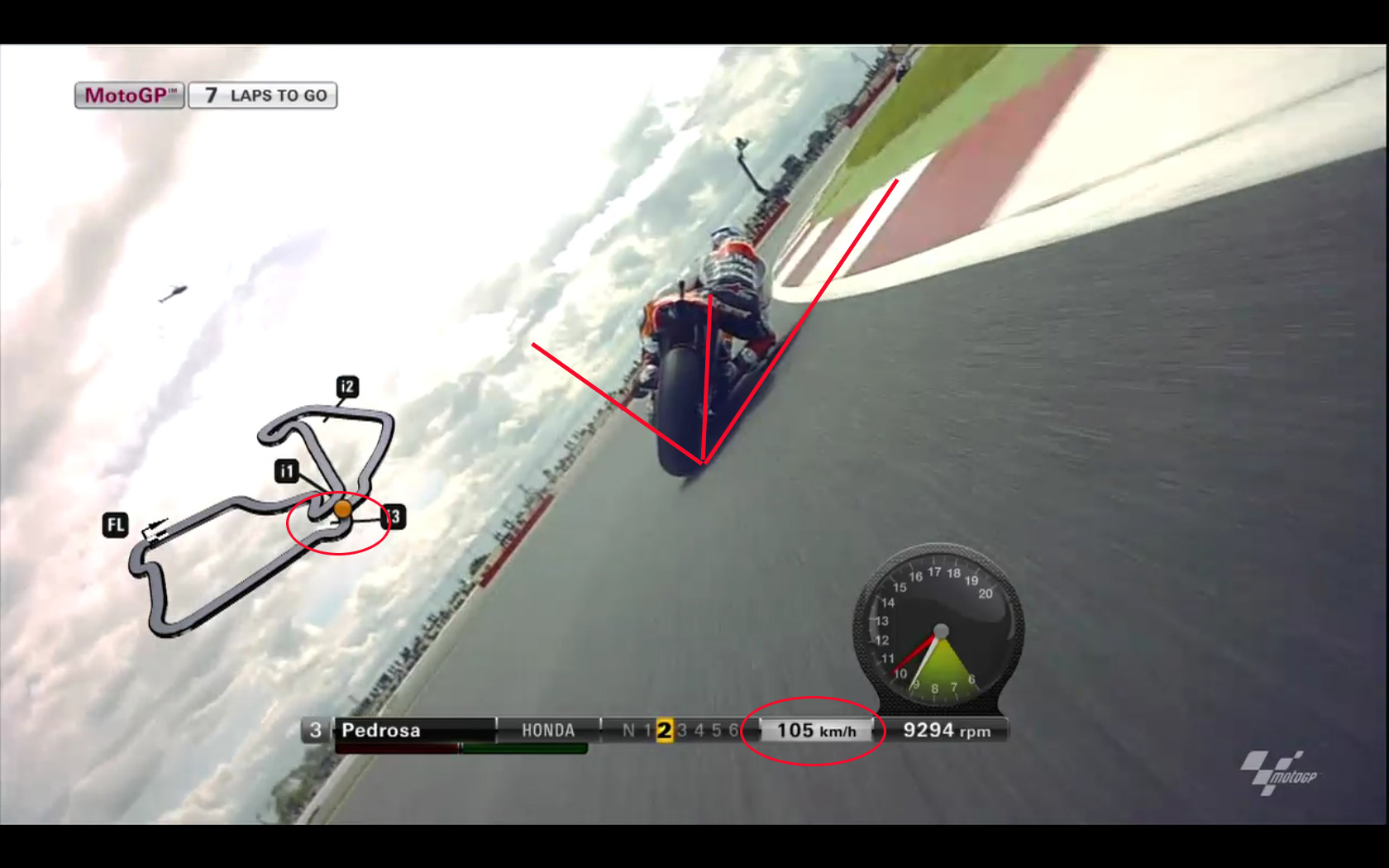
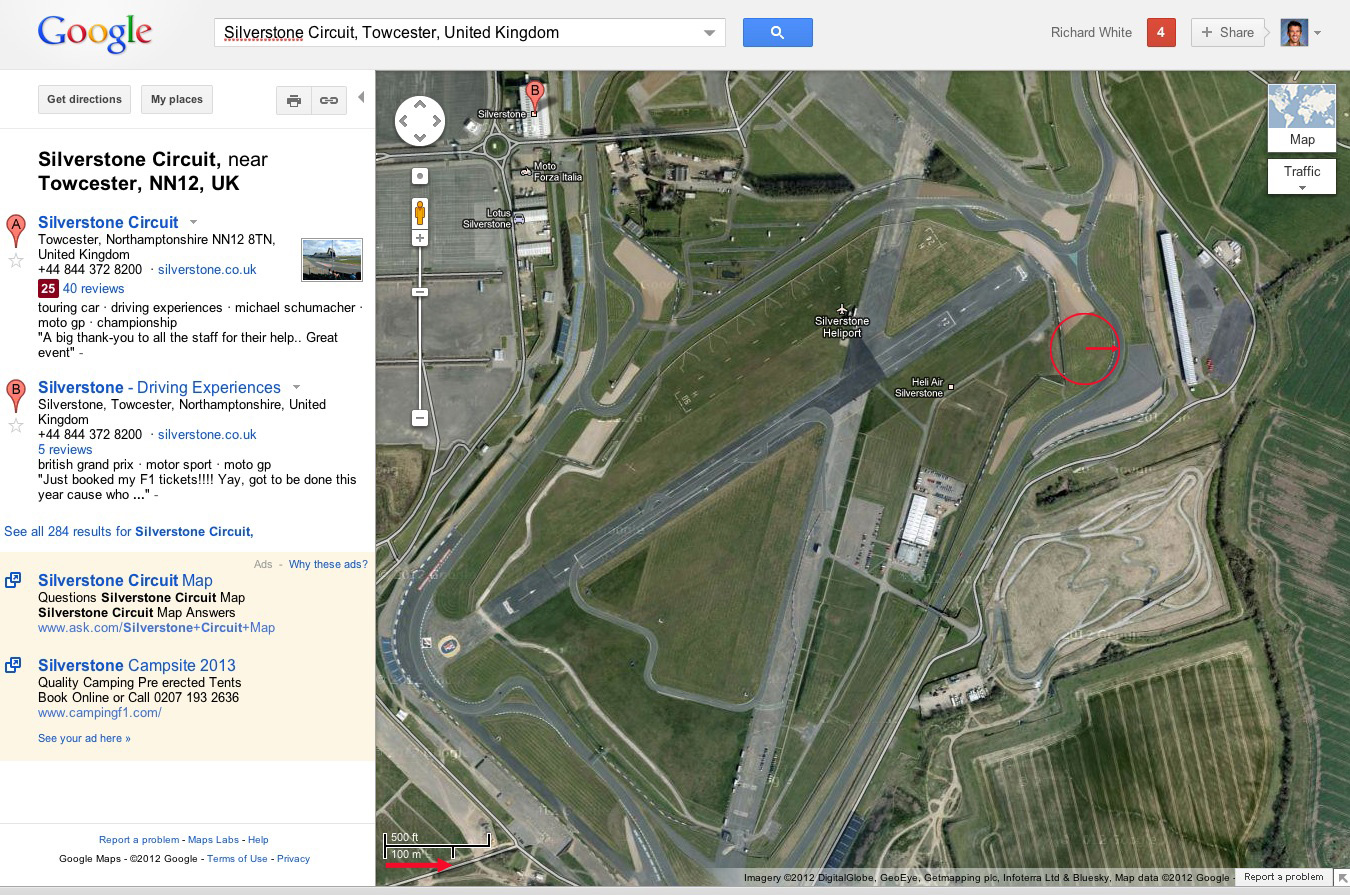
Based on information gained from these preliminary analyses, determine the coefficient of static friction between the motorcycle's tires and the road.
Carefully explain and document your reasoning, in words and calculations, and comment on how reasonable you think your results are.
3. Water as Projectile Motion
- Have someone take a digital picture or video which clearly shows you, a measuring device of some type, and some type of water projected at an angle into the air. This might be a jet of water coming from a garden hose, a syringe or water-cannon shooting water, a straw held at some angle through which you blow a mouthful of water, or even a large cup of water that you use to throw the water across a yard, driveway, or sidewalk.
- By analyzing the photo/video and using the measuring device as a scale, you can make various length measurements (horizontal and vertical) to help you solve the other parts of this problem. Draw on the photo any lines or guides that indicate measurements you are using in your analysis. Note you are taking no TIME data.
- Use your measurements (not a protractor) to calculate the x and y components of the water's velocity at the point where the water leaves the source.
- Calculate the amount of time it takes for the water to reach its highest point.
- Determine the angle (relative to the horizontal) of the initial velocity at the point where the water leaves the source by two different methods, and calculate the percent difference between the two values.
Method 1: Measure the angle on the photograph using a protractor.
Method 2: Calculate the angle based on your answers to part c.
- Develop a single equation to describe the water's trajectory (x and y coordinates) as a function of time, and express it using i, j notation.
4. Friction on a Jet Sled
Lovely Grizzelda, Poly's super-star physics student, has built a jet sled. Its power supply provides a force equal to 5 times the weight of the sled. Problem is, the rails upon which the sled travels provides a frictional force that is directly proportional to the sled's velocity.
- Derive an expression for the sled's maximum speed. It is OK if this includes an undefined constant.
- Derive an expression for the sled's velocity as a function of time, assume it starts from rest. Put the final solution in terms of your answer in Part a.
- Use the relationship derived in Part b to determine the velocity of the sled at: i.) t = 0; and ii.) t = infinity.
- Derive an expression for the sled's position as a function of time, assuming it starts at the origin.
- Use the relationship you derived in Part d to determine the coordinate of the sled at t = 0.
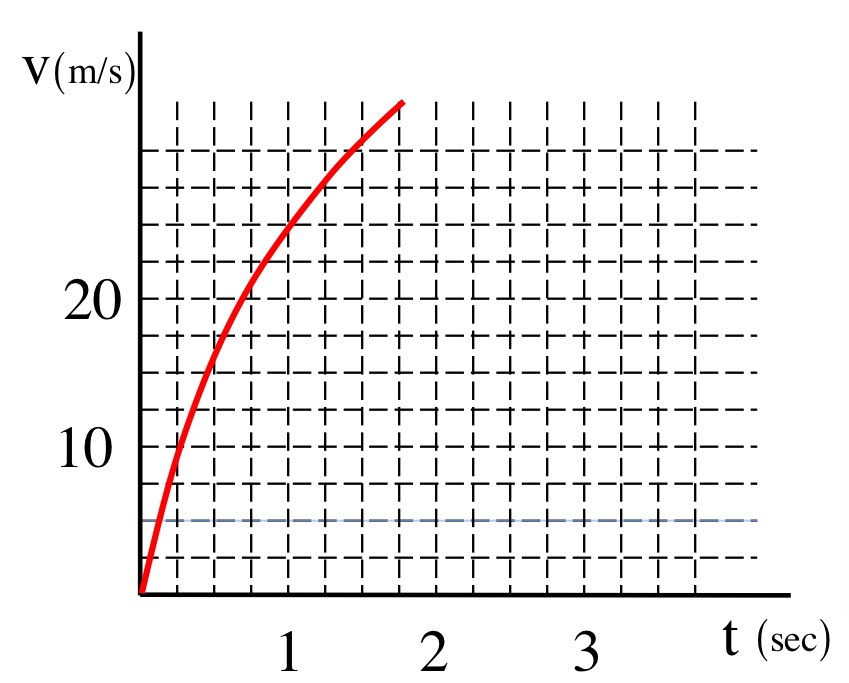 You are given a graph of the velocity as a function of time, but the graph is not complete. Assuming the mass of the sled is 600 kg, use the information provided to determine the value of the "undefined constant" alluded to in Part a.
You are given a graph of the velocity as a function of time, but the graph is not complete. Assuming the mass of the sled is 600 kg, use the information provided to determine the value of the "undefined constant" alluded to in Part a.
5. Kaylee Goes Skydiving

Kaylee decides to go skydiving, and she'd like you to make the jump with her (and solve some physics problems along the way).
- Identify your mass.
- What is the force of gravity in Newtons acting on you just before the plane takes off (at the surface of the earth)? (The acceleration due to gravity in the Los Angeles area is approximately 9.796 m/s2. Calculate to four sig figs.)
- According to Newton's Law of Universal Gravitation, what is the force of gravity in Newtons acting on you at the jump height of 14,000 feet? (Calculate to four sig figs.) What is the percent difference between your weight at the two different heights?
- The density of the atmosphere varies with altitude. Perform some research that will allow you to determine a function that describes the density of the atmosphere as a function of altitude for the Troposphere, that portion of the atmosphere through which you are performing your skydive. (Be sure to cite your source URL if accessing a webpage, and the date that page was accessed.)
Note that if you can't find a function that will work for you, you can take data from this page and create your own exponential function using a regression.
- You jump from the plane at a height of 14,000 feet with an initial vertical velocity of 0, where the air density has been determined above. The Resistive force of fluid friction on you as you fall is described by the equation:
R = (1/2) DρAv2
where
- D = drag coefficient, a dimensionless quantity determined empirically
- ρ = density of air
- A = cross-sectional area (of surface exposed to air)
- v = instantaneous velocity
Assuming some amount of air friction R is acting on you as you fall, draw a free-body diagram of yourself for a time before you have reached terminal velocity.
- Based on your research, identify a reasonable estimate for your drag coefficient and a reasonable estimate of your cross-sectional area.
- Assume that at one point, you have a downward velocity of 25.0 m/s at a height of 3,000.0 meters. Based on your calculations, identify the magnitude and direction of your acceleration at that instant.
- [Challenging] We'd like to calculate your velocity as you fall, but we have an issue: the net force acting on you (including drag) determines your acceleration, which determines your velocity, which affects the net force acting on you, which determines your acceleration, which determines your velocity, which...
Use Euler's method, along with a spreadsheet analysis, to determine one of two values:
- Your terminal velocity before you pull the parachute, or
- Your velocity just before you hit the ground (not having pulled the parachute).
Please note that Kaylee did safely land with a parachute when she performed this experiment.
For information on how to solve this problem, you might consult any of the relevant explanations on YouTube. My favorite is this one from Flipping Physics.
The spreadsheet you use to solve this problem should include clear titles and documenting cells, and shared/emailed to your instructor, as well as being printed and included with your paper solution.



 You are given a graph of the velocity as a function of time, but the graph is not complete. Assuming the mass of the sled is 600 kg, use the information provided to determine the value of the "undefined constant" alluded to in Part a.
You are given a graph of the velocity as a function of time, but the graph is not complete. Assuming the mass of the sled is 600 kg, use the information provided to determine the value of the "undefined constant" alluded to in Part a.