Extra Credit #1

Begins Friday, Oct 14, 2022

Ends Monday, Oct 24, 2021

The purpose of this assignment is to allow students to demonstrate their understanding of various abstract and applied physics topics. Because of the nature of this assignment, it will be graded fairly strictly—pay close attention to the Notes below. Assignments which are not completed as required will not be evaluated.

NOTES:

The Extra Credit Assignment consists of five problems, to be completed outside of class.
This assignment is Extra Credit and not required.

This assignment is intended to provide students with the opportunity to review some of the material we've covered, and not all students need the same amount of review. Students will be eligible to receive credit on problems completed according to the table below.

Your Test Average (incl. Ch 5-6 test)	Review Problems You Are Eligible to Complete
0 - 79%	Problems #1 -4
80 - 89%	Problems #2 -4
90 - 100%	Problems #3 -4

The total points earned by a student on this assignment will be determined by the instructor based on a number of factors, including number of problems completed, difficulty of problem, and overall quality of assignments submitted by students.
You may work on the problems with other people—in fact, this is encouraged—but each person must complete his or her own assignment to be turned in. Even when numeric answers to problems are the same, solutions from different students must be written independently, and differently, and developed and explained in each student's own words.
The assignment must have a separate cover sheet that includes Your Name, Date, Course and Period, Name of Assignment and the SPECIFIC NUMBERS ATTEMPTED. Staple this cover sheet to the front of the problems that you've solved.
Each response must be hand-written on a separate piece of paper, which must include:
a) Your name and the problem number at the top of the page.
b) Salient details from the original question written out as appropriate (blurbs).
c) Your solution, hand-written in blue or black ink (pencil is OK as long as it's DARK), with all work shown in detail.
d) Drawings, diagrams, or graphs with labels must be used to explain your solution more clearly.
e) Written explanations (blurbs, in English) explaining important steps in your solution.
f) The final answer, with a box around it.

See below for an example.

If this seems like an awful lot of work, it is! Remember that this is Extra Credit: you're trying to impress the instructor with how well you can do. If in doubt, do a little more than you think you should, rather than trying to get by with less, at the risk of losing points on your solution.
The assignment will be available online on Friday, Oct 8 (though you have a test on the 12th--I'd suggest you concentrate on it before starting this!).
The instructor will be available to answer questions about the assignment on a limited basis: before school, after school, and possibly by e-mail. The instructor will not be able to help you if you leave all of your work until the night before the assignment is due.
Your completed assignment must be turned in directly to the instructor anytime before 3:00 PM on Friday, October 22, 2021.

EXAMPLE PROBLEM AND SOLUTION:

SAMPLE PROBLEM:

In "The Matrix," Neo is given a test by Morpheus, who asks him to leap from the top of one building to another. Assume the buildings are each 100m tall, and 15m apart. Neo runs and leaps from the first building with a velocity of 5.00 m/s at an angle of 36.9 degrees (toward the second building).

a. Will he make it to the next building?
b. Where exactly will Neo land?

(Assume no air friction in this problem.)

EXTRA CREDIT PROBLEMS

1. Volleyball Serve

Watch the video of Becca Hanel serving a volleyball. Using time data taken from the video (which runs at 30 frames per second) and reasonable distance/length estimations, calculate the initial velocity of the ball as it is served.

Carefully explain and document your reasoning, in words and calculations.

2. Motorcycle's Coefficient of Friction

In the 2012 MotoGP race in Silverstone England, TV coverage provided data for some motorcycles' position on the racetrack and speed at that location (see video clip) . By taking some screenshots, searching on Google Maps for the racetrack, and using Adobe Photoshop layers, I (Mr. White) was able to do some additional graphical analysis (shown here).

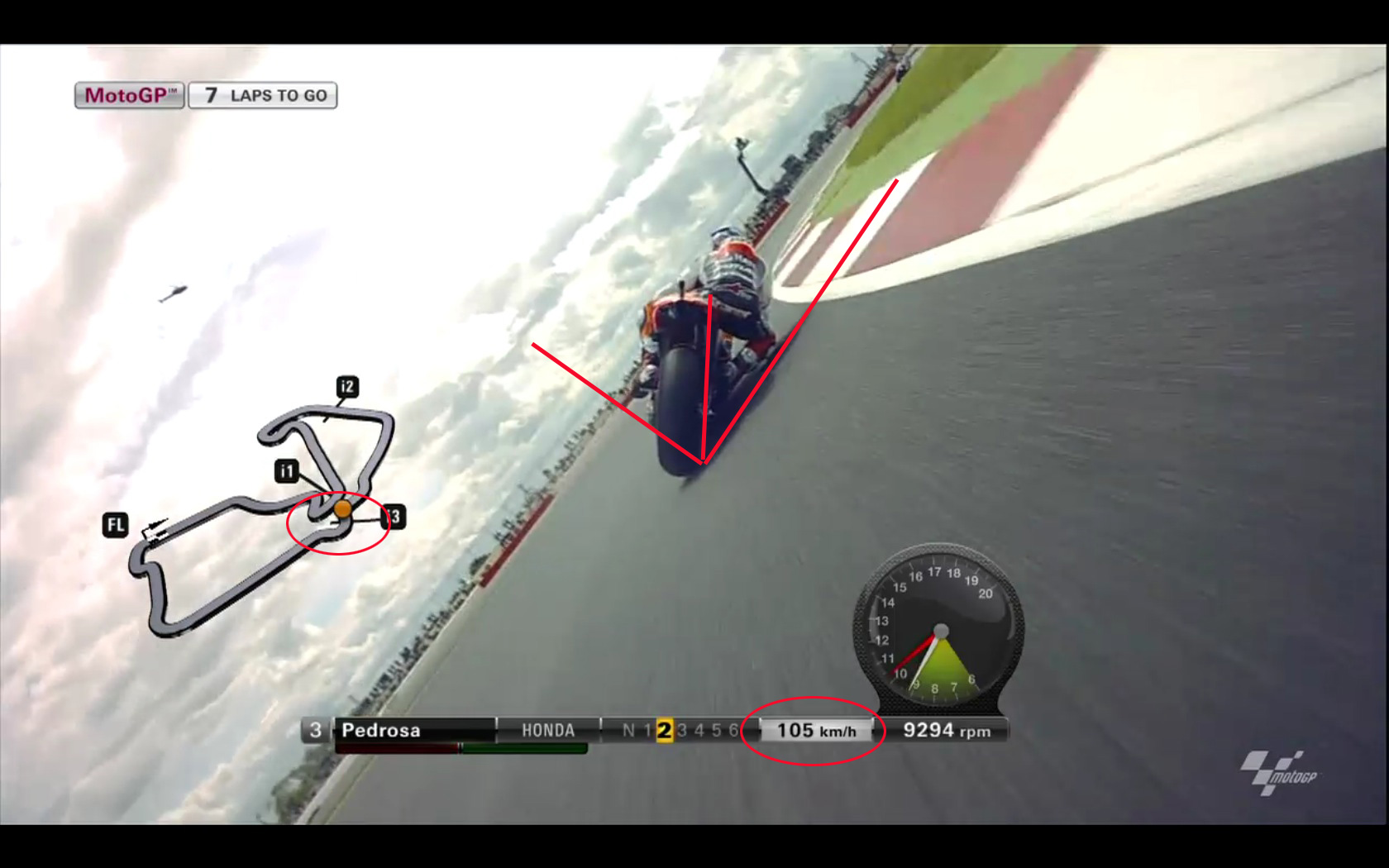
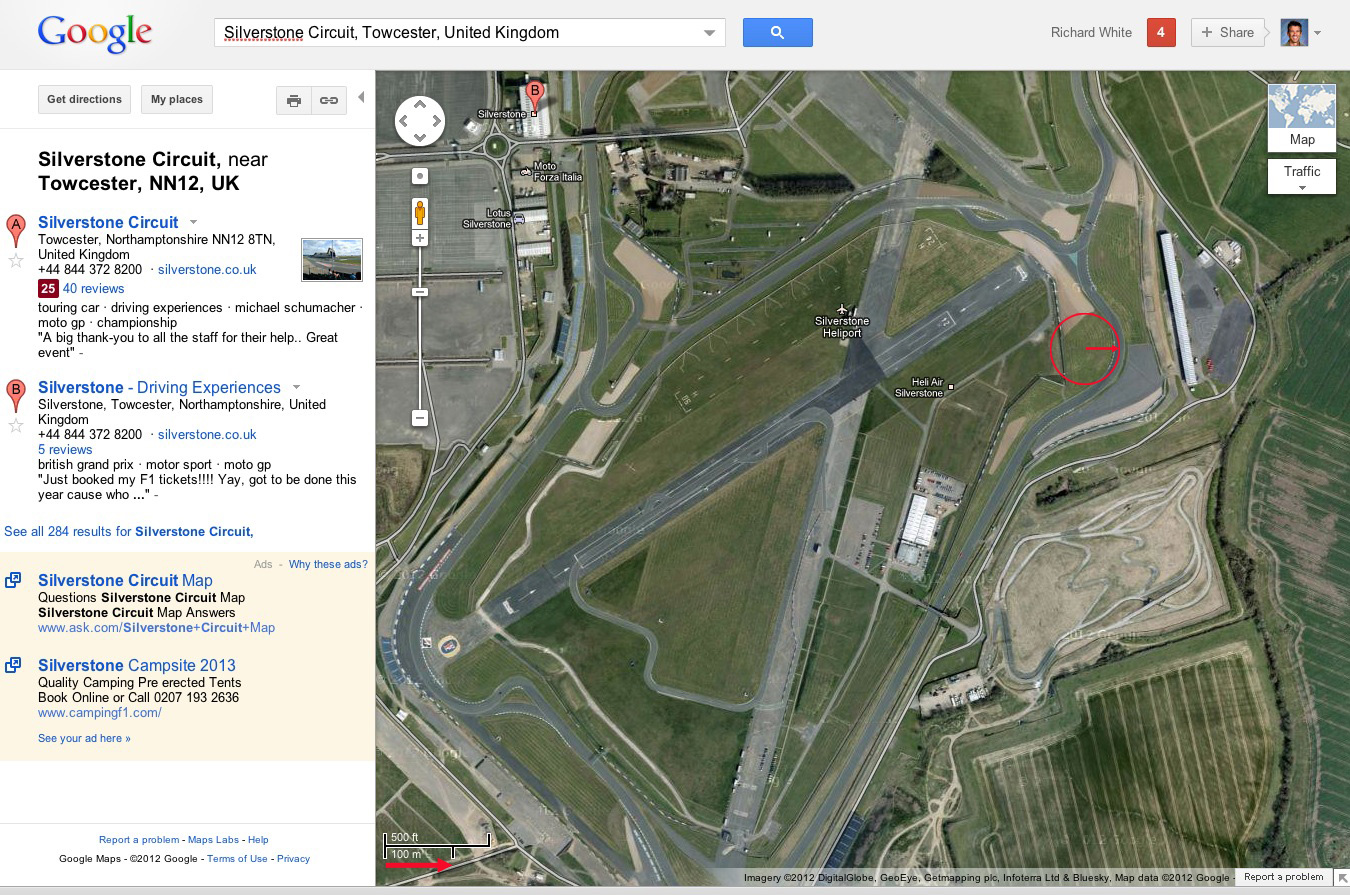
Based on information gained from these preliminary analyses, determine the coefficient of static friction between the motorcycle's tires and the road.

Carefully explain and document your reasoning, in words and calculations, and comment on how reasonable you think your results are.

3. Water Spout

Take a digital picture which clearly shows some kind of spouting water. It can be a drinking fountain at Polytechnic or you holding a hose at home or whatever clever thing you would like, but it must have water spouting upward and outward from you in a demonstrable way. The picture should include your face, the water's full trajectory as it leaves the device producing it and at least part of a vertically oriented meter stick. By printing this picture and using the meterstick as a scale, you can make various length measurements (horizontal and vertical) to help you solve the other parts of this problem. It's appropriate for you to draw on the photo any lines or guides that will indicate measurements you made using the photo.
Using these measurements (and not a protractor, so you can't assume you know the angle), calculate the x and y components of the water's velocity at the point where the water leaves the fountain.
Calculate the amount of time it takes for the water to reach its highest point.
Determine the angle (relative to the horizontal) of the initial velocity at the point where the water leaves the fountain nozzle by two different methods, and compare the two values.
Method 1: Measure the angle on the photograph using a protractor.

Method 2: Calculate the angle based on your answers to Part 2.
Develop an equation to describe the water's trajectory (x and y coordinates) as a function of time using "i" and "j" notation.

4. Friction on a Jet Sled

Lovely Grizzelda, Poly's super-star physics student, has built a jet sled. Its power supply provides a force equal to 5 times the weight of the sled. Problem is, the rails upon which the sled travels provides a frictional force that is directly proportional to the sled's velocity.

Derive an expression for the sled's maximum speed. It is OK if this includes an undefined constant.
Derive an expression for the sled's velocity as a function of time, assume it starts from rest. Put the final solution in terms of your answer in Part a.
Use the relationship derived in Part b to determine the velocity of the sled at: i.) t = 0; and ii.) t = infinity.
Derive an expression for the sled's position as a function of time, assuming it starts at the origin.
Use the relationship you derived in Part d to determine the coordinate of the sled at t = 0 (note that you are doing this to see if your function in "d" makes sense).
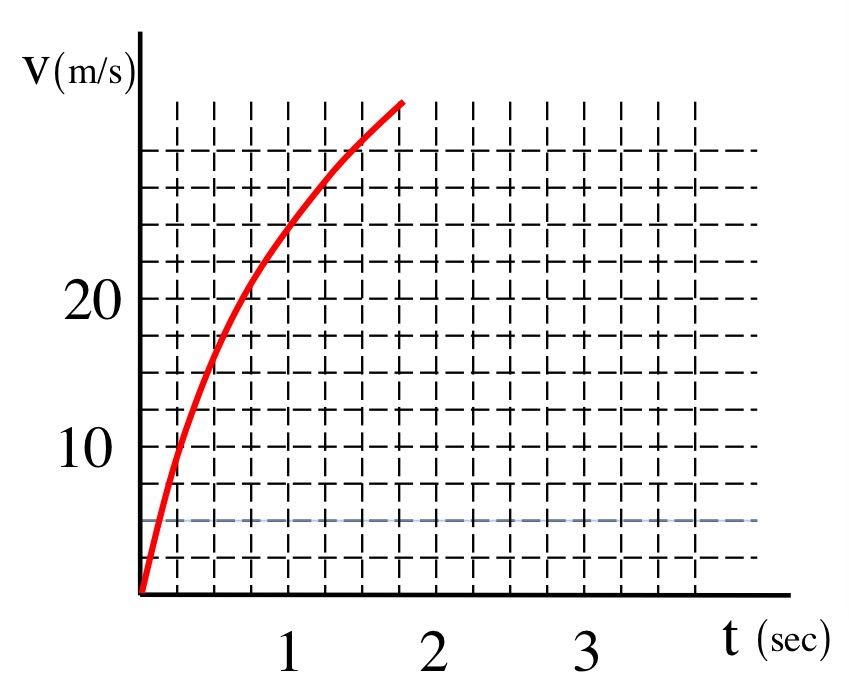You are given a graph of the velocity as a function of time, but the graph is not complete. Assuming the mass of the sled is 600 kg, use the information provided to determine the value of the "undefined constant" alluded to in Part a